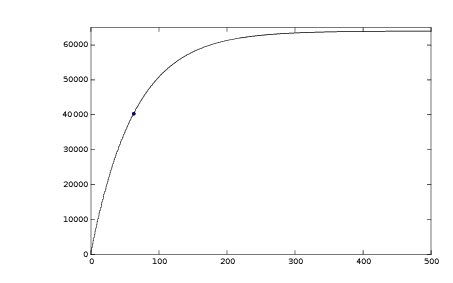
A micro controller can process a low pass filter function, however floating point and even integer multiplication can take too much time to be useful. The following approach uses shifts instead of multiplication. See the project log.
Integer low pass filter
A lowpass filter algorithm for small controllers without multiplier

 Bruce Land
Bruce Land
 MS-BOSS
MS-BOSS
 agp.cooper
agp.cooper